The stage is set. We started building the energy transfer model (ETM), and we’ve talked about the flavors of energy. We are ready for a new representation to help us start thinking about energy storage in a system. In a day or two, we’ll be using energy bar charts, but first, we’ll get used to thinking about energy storage with a simpler, stepping stone diagram.
Diagram Attributes
I will run through the typical way I introduce the diagram in class in just a minute. First, here’s the teacher preview of some key energy pie chart features.
Before doing anything else, list the objects in your system. The diagram will only make sense in the context of your chosen system, so you need to be explicit about that. Teacher note: if you want students to pick up the habit of defining a system first, you need to be very careful to always do it that way yourself.
The size of the pie matters. The size of the pie determines the total amount of energy stored in the system. So, if the pie becomes larger, there is now more energy stored in the system. If the pie becomes smaller, there is now less energy stored in the system.
The size of a slice doesn’t matter on its own. Whether the slice has grown, shrunk, or stayed the same between snapshots is what matters. Students don’t have energy equations yet. They know what each flavor of energy depends on (per the flavors of energy discussion immediately before this activity), so they should have ideas like, for example, kinetic energy will be bigger if the object is moving faster. They don’t have a way of reasoning, yet, about whether the kinetic energy should take up half of the pie or a quarter of the pie at any particular snapshot. We’re looking to show how the energy storage changes, not what it necessarily is. Energy is boring. Change in energy is interesting.
For the situations we’re going to encounter, represent, and analyze in this class, we would be surprised to see energy being stored as Etherm in one snapshot, then stored as Kinetic or Gravitational energy in a subsequent snapshot. For our purposes, when there is a ∆Etherm, the energy is essentially “stuck” that way. We’ll never get to use that slice of the pie again. That slice of the pie is dead to us. It might get larger, but it will never get smaller. Since it’s a dead part of the pie, instead of writing ∆Etherm over and over again, we can just shade it in. We’ll all know what that means.
Introduction of diagram
Right. Ready for a new representation to add to our arsenal? When’s the last time you drew a pie chart? Third grade? (Students: Yep, that sounds about right. Back with the bar charts.) Okay, but these pie charts are going to be a little more sophisticated than what you were drawing back in the day.
Just inside the packet there’s a page with some energy pie chart practice. We’re going to do the first one together. Actually, we’re going to do the first one together twice. After that, I think you’ll get the idea, and I’ll let you argue the rest of them out without me.
So the problem is a ball being dropped to the ground, right? I think it looks like this? [I’m drawing the diagram on the board, but having done this problem at least 15 or 20 times by now, I don’t have the packet in my hands.] And it has a sort of motion map next to it, right? The arrows are supposed to be showing how fast the ball is moving at that snapshot. The dot means it isn’t moving.
The first thing we need to do is define what we’re saying is in our system. Let’s put all the objects that store energy into our system. We could put the entire universe in our system, but that seems a little overkill. Can we narrow it down to just the relevant objects for this problem? (Likely answers: The ball. The ground. The air.) I think you’re missing something. Something really big. (Oh, the Earth.) Okay. Does the ground store energy? (Yes. Wait, it doesn’t hit the ground. So no?) So we probably don’t need the ground. It won’t change anything to include it, if it doesn’t store energy, but we don’t really need it. Why does the air store energy? (Air resistance.) Okay, so question—from how high above the ground is this ball being dropped? (It doesn’t say.) Let’s do it twice, then. Let’s do it the first time with it being dropped in this room. Then we can come back to it a second time and consider it being dropped from the Sears Tower. (I don’t think it’s called that anymore.) Okay, the second time we’ll do it being dropped from the Sears Tower in 1992, when I know for sure it was still called the Sears Tower. When we are dropping it in this room, what do you think about the air resistance? Will it be significant? (Probably not.) So we don’t need the air in our system right now, but we will need it on the second time through.
Okay. We’ve got our system now! Ball and Earth. There are three snapshots shown in the picture, so we’ll draw three pies. We put all of the objects that would store energy into our system, so the total energy should stay the same. In the future, we could have the total energy changing, but while we are practicing this diagram for the first time, let’s try to keep it so the total energy stays the same. So we don’t have to keep track of too many new things all at once. So if the total energy is the same, then the size of the pie should always be the same.
Everyone’s favorite—drawing circles! We need to draw three circles that are all about the same size. [I start drawing my totally inadequate circles on the board. The flavors of energy chart is still up on the board next to the circles, for easy reference for the next part.]
Oh! Big warning! Do NOT write this next part down yet! Trust me, you’ll just get really angry with me if you write it down now. You’ll be able to write it down at the end.
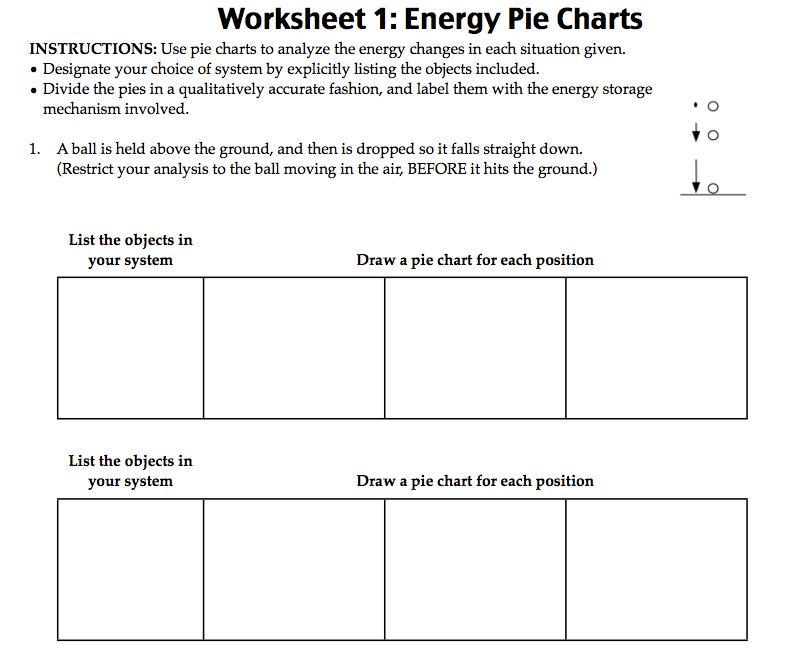
Alright! Finally! Now, it’s time to play the Energy Pie Chart Game! Who wants to go first? [Choose an arbitrary kid who is excited to play the “game” even though they don’t know what it is yet. Let’s call the first kid Brandon.]
Great! Brandon, what’s your favorite flavor of energy, besides thermal? [You want to do thermal energy last. Trust me. You’ll see in a minute.] (Uh, gravitational interaction energy, I guess?) Super! In the first snapshot, is there any energy being stored as Ug? (Yes.) [I section off a corner of the pie and label it Ug on the board.]
Okay, second snapshot. Does the amount of energy stored as Ug get bigger, smaller, or stay the same? (It’s smaller.) [I section off a smaller chunk of the pie for Ug in the second pie.]
Final snapshot. Does the amount of energy stored as Ug get bigger, smaller, or stay the same? (Smaller.) [I start sectioning off a still smaller slice for the third pie. If the class (or Brandon himself) hasn’t steered us off toward needing a y = 0 m line yet, it usually happens at this point as some think there should be no Ug in the third pie, but others think there should. At whatever point seems reasonable, there’s a discussion of needing to agree where Ug will be zero and the drawing of a y = 0 m line on the picture. Most classes decide that the ball is above the ground, that they want the y = 0 m line on the ground, and that there is therefore still some Ug left at the end. It really doesn’t matter what they decide as long as it is consistent and makes sense to them. It’s probably not a good idea to put the y = 0 m line above the object because, while a negative amount of Ug is fine, it’s really tough to draw a negative slice of a pie (and hurts your brain a bit to even think about).]
Thank you for playing! who wants to play next? Zoe? Great! What’s your favorite flavor of energy (not thermal)? (Okay, spring energy.) Fantastic! In the first pie, is there any energy stored as spring interaction energy? (No.) Second pie: does the amount of energy stored as Us get bigger, smaller, or stay the same? (There’s still none.) Third pie: does the amount of energy stored as Us get bigger, smaller, or stay the same? (None again.) Excellent, thank you for playing!
Next! Kirstin. What’s your favorite flavor of energy (not thermal)? (I guess it must be kinetic energy, then.) A fine choice. Okay, first pie. Is there any energy stored as kinetic energy? (Well, it’s not moving, so no.)
Okay, second pie. Does the amount of energy stored as kinetic energy increase, decrease, or stay the same? (It increases.) [I add a section of Kinetic energy to the second pie. It doesn’t matter how much. Students might get concerned about how big the kinetic slice should be compared to the Ug slice, but they have no way of making that comparison yet, so it really doesn’t matter. It just matters that the K slice has gotten larger and the Ug slice has gotten smaller since the first pie.]
Third pie. Does the amount of energy stored as kinetic increase, decrease, or stay the same? (Increase.) [I draw a larger slice of K in the final pie.]

Thank you so much for playing! Next! Victor. What’s your favorite flavor of energy? (That would be change in thermal energy.) Aces.
Is there any interaction that would cause energy to be stored as thermal energy between the first pie and the first pie? (No. Wait, what?) Remember that we’re always talking about ∆Etherm, not Etherm itself, so we will always have to keep comparing the current snapshot back to the first snapshot. (Aha.) So, could there ever be ∆Etherm in the first pie? (No.) Sweet.
Okay, second pie. Has there been any interaction that would cause energy to be stored as thermal energy between the first pie and the second pie? (Well, no.) How about between the second pie and the third pie? (Does it hit the ground? Oh, it doesn’t. So, no.) Alright! Thanks for playing!
So that’s it, right? We’re finished? [Look at the board and see the weird-looking pies with blank slices.] Okay, there’s clearly something weird going on. When we started, we didn’t know how much of the pie each slice would take, so we didn’t end up using the whole pie. Is there anything outside the system that would take energy out or put energy in? (No, we put everything that mattered in the system.) Okay, so the total energy must stay the same. So we just need to redistribute the slices so that we take up the whole pie each time.
And now you see why I told you that you probably didn’t want to write this down while we did it, right? [At which point, the kid who didn’t listen to that is grumbling while reaching for an eraser, but also can only really blame himself.]
Okay, we just need to make sure that we keep the idea of whether the slices get bigger or smaller. The first pie has only Ug, so that must be the entire pie. The second pie has Ug and K. We don’t know whether more energy is stored as Ug or as K yet, but we know that Ug is smaller than it was before. [Usually, they want to make it half and half. Even though they wouldn’t agree with that in a couple of days, it really doesn’t matter here, so I go with what they want.] Final pie, we know Ug has to be even smaller and the rest has to be K. [They usually want a very little slice because the ball is just barely above the ground (which is usually their y = 0 m line).]

That looks a lot better, huh?
And—we’re finished! Okay, should we try that one again?
One more time
[The second time through is much faster. They have a second space to write the new version of the problem, but I usually just modify what was on the board—that makes more sense for the class conversation, anyway. The new version of the problem is to drop the ball from much, much, much higher (the Sears Tower in 1992) so that we have to take the effects of air into account.
We quickly decide that the main thing that will be different is that we now have an interaction between snapshots that causes energy to be stored as thermal. That is, there is now some ∆Etherm. Let’s join the conversation back at that point, when they’ve decided what is different is that there is now some ∆Etherm.]
Okay, let’s give Victor another shot at playing the pie chart game.
Victor, is there any interaction between the first pie and the first pie that would cause some energy to be stored as thermal? (Yes. No, wait, no. Not in the first pie.) Can you ever have a change in Etherm in the first pie? (No, that doesn’t make sense.)
Okay, is there any interaction between the first pie and the second pie that would cause some energy to be stored as thermal? (Yes. Air resistance.) Why does that cause a change in Etherm? (The ball is hitting the air.) [Reference back to the matter model and look at what happens to the particles when you hit the matter models together. Faster random motion. ∆Etherm.] Great, so we need to take a slice of the pie back and make it ∆Etherm. Do you think we should take it out of Ug or out of K? [Good, brief discussion usually happens here. We settle in on taking it out of K because with air resistance, it wouldn’t be moving as fast as it would have without air resistance. I section off a part of the K slice, but I don’t label it yet. I pause.]
Remember earlier when we were first talking about thermal energy? We said that we never see a box start suddenly sliding across a table while everything gets colder. In fact, once the energy ends up stored as thermal, it’s usually kind of stuck there. At least, in most of the simple examples we’re thinking about right now, that’s true. Right? It’s tough to get the energy that is stored as Etherm to be stored as another flavor of energy. Basically, if any slice of the pie represents ∆Etherm, that part of the pie is going to stay that way for the rest of the problem. It sort of becomes dead to us. So knowing that, it will be pretty easy to just shade in any part of the pie that represents ∆Etherm. We’ll all know that it means it’s the dead part of the pie. [So now I shade in the ∆Etherm slice instead of labeling it.]
Last one. Third pie. Is there any interaction that happens between the second and third pie that would cause even more energy to be stored as thermal energy? (Yes, it keeps hitting the air.) So is the amount of ∆Etherm bigger, smaller, or the same as the second pie? (It’s bigger.) Could it be smaller? (No, it has to stay ∆Etherm.) Right—there might be some cases where that happens, but not in the situations with simple objects that we’re looking at right now. [We decide to slice out the kinetic energy again, and I shade in the last slice. On the whiteboard, I just draw diagonal lines to “shade” the area instead of using all of that ink, but they tend to color it in when they are using pencil.]

That’s great, everyone! Do you get the general idea so far with pie charts? (Yep.) Wonderful. There are a bunch more problems on this page and the next one to get some pie chart practice and a deeper understanding of what’s going on with energy storage. My recommendation would be to work in groups and to do the problems on the whiteboards at your tables first so that you can try out your division of slices and erase to make revisions without getting frustrated about having to erase so much on the paper. You can do whatever works for you, though. Let’s work on these for a bit, then we’ll whiteboard.
Okay, you’re ready for me to stop talking now, right? [At this point, most of them probably aren’t listening to me anymore anyway. They’re grabbing markers or fighting out the next problem with their groups, already.]



I like how you’ve shaded ∆E_{therm} in your pie charts, indicating that it’s not super useful. Since you’ve clearly thought a lot about this approach, I’ll ask: Why use ∆E_{therm} instead of E_{therm} itself?
We talk about that when we talk about ∆Etherm (with the rest of the flavors of energy). The thinking is that every object has a whole bunch of Etherm already. The amount it changes isn’t very much, actually, compared to how much it is already storing before, say, a ball bounces on a table. Also, we don’t have any way of really thinking about how much is there already being stored. In any case, energy is boring, change in energy is interesting. The amount the thermal energy changes is something we can think about and represent (and seems to be important for representing things like boxes sliding across a table, etc). So for Etherm, we always talk about ∆Etherm instead.
Because of that, we never have to include it on an initial pie chart, in the first L of an LOL, etc. We also don’t forget that there was already a bunch of Etherm stored there because we’re never saying the initial Etherm is 0 J.
Does that make sense? What do you think?
It makes perfect sense. I’m only worried in that I’d like the representations to be robust enough to cope with thermal processes like heating. Since pie charts are just a bridging representation to bar graphs, perhaps that’s a little too much to expect? I’ve never liked energy pie charts (or bar graphs) because for everything but gravity, only changes matter, as you said. An alternative to having a pie chart with almost all thermal energy would be too include it as a reasonable fraction but have it grow, since we can set Energy=0 wherever we want. It would also save having to redraw that first energy pie chart. 😉 The students have no idea of the relative Etherm versus Emech anyway, and perhaps I’m too simple-minded to like the asymmetry in the treatment of different energy storage forms.
Perhaps it would be too abstract, but if only differences in energy really matter, then it might be possible to do an energy transfer model with only the “O” in LOL, quantifying transfers in and out of the system. We could look at ∆Etherm, ∆K, ∆Ug, ∆Us, etc. I think the point is that this makes energy too abstract, and I tend to agree. If it is too abstract, I’d just as soon develop some concept of absolute (as opposed to relative) Etherm. However, in this I’m just rambling, so I should probably go look at some relevant PER.
We definitely represent heating on LOLs. You could also certainly represent changes in total energy with pie charts by changing the size of the pie as the total energy increased or decreased. In Honors Physics, we only spend about 40 minutes total on pie charts.
I think you might be underestimating the students, though, with respect to understanding how much of the pie Etherm should take up. It wouldn’t take them long to come up with that idea. Consider this very simple problem—a box slides across a table and comes to a stop. All of the initial K ends up stored as Etherm. The change in temperature of the box and table is so small that you can’t feel it with the temperature sensors in your hands. On the other hand, they know the thermal energy already stored in the box/table has to do with the temperature it already was, and they can feel the difference in temperature between the box/table that had been sitting in a cold room vs a hot room. So, obviously, there was already a ton of Etherm stored in the box/table in the regular temperature room. They already have the idea that Etherm has to do with the random motion of the particles in the object, and they also have the idea that the particles are already moving a lot before the box does the slide across the table. In any case, the relevant thing was that the random motion of the particles (something we can’t measure very easily) has changed by a discrete amount from snapshot to snapshot.
Okay, here, when you are talking about the system in the bar chart, you’re mixing up changes in total energy with changes in the way energy is stored within the system. You’d never represent a change in kinetic energy, thermal energy, gravitational energy, or spring energy (or any other flavor of energy) on the system of the energy bar chart. You only represent work, heat, or radiation being done to the system there. Energy does not enter or leave the system as any particular flavor of energy. This sort of subtlety and confusion is exactly what the bar charts are great at helping and why they’ve had such a huge impact on my students’ understanding of energy transfer! 🙂 But I think you’re not really even thinking about work/heat/radiation in that paragraph. I think you’re bringing it back to an equation and away from a graphical representation. I’ve taught it that way, too, and it doesn’t even compare to what students can do (and explain and understand) with graphical representations. You can read more about that in my LOL post.
Yeah, you’re totally right about the system part. That’s just transfer across the system boundary. In order to do what I was suggesting, that center “O” would have to be divided into subsystems (maybe a schematic pie chart) with arrows sloshing energy around inside, which would get a little crazy. Trying to account for where energy went (both internally and externally) would be fruitless. Thanks for putting my head on straight.
Thanks for the post Kelly. I am interested in your reasoning for including pie charts at all; bvancil mentioned above that they are ‘just a bridging representation to bar graphs.’
That’s a good question. I’m not sure I would call them “bridging” because I’m not sure what the bridge is being built between. I do call them a stepping stone tool in the post, which they definitely are. In Honors Physics, we probably spend a total of about 40 minutes with pie charts. In the regular class, probably 60 to 80 minutes. A few students find them a useful tool moving forward and do keep drawing them occasionally throughout the year.
Admittedly, I haven’t tried jumping straight to LOLs without the pie charts, but I can tell you what I think I’m gaining from those one or two class periods.
Pie charts are the first time students try to represent the changes in how energy is stored. It’s the first time they are thinking about the different flavors of energy at all. It’s a lot for them to process, just deciding how the energy is stored in each snapshot, etc. They do a lot of erasing on these few problems.
LOLs show the same sorts of things, but for them to be the sharp, powerful diagram that I think they are for the rest of the year, they need to be very careful and intentional in several aspects of their drawings. They need to count boxes in each L to make sure that the total amount of energy stays the same. They need to show changes in total energy by having arrows entering or leaving their system. There are a lot of labels and details.
So the pie charts are basically a simpler sandbox for letting students play with the energy concepts. When they get to LOLs the next day, they come to them having already built some skill in thinking about the big picture. They are ready to add in some details. And there’s a lot less erasing (so, a little less frustration).
What do you think?
That answers my question perfectly. Not really necesary, but helpful to making the transition to bar charts. I’ll have to do some thinking before I decide what to do with my ‘honors’ kids, but I think I will do them for regular.
Hey Kelly!
Interesting ideas! I have stopped giving students the rules for pie charts. Instead, the play the phet energy skate park and tell me the rules. Works pretty well.
Btw, do you do anything to get across the definition of energy? Something along the lines of impact testing from different heights?
How long do you spend on pie charts total (including using the computers, working on the problems, any homework involved, and doing the whiteboarding)?
Before we get to pie charts, we’ve already defined change in energy as the thing that’s different about a spring when it’s more stretched vs less stretched (and, through the experiment, we’ve also defined change in energy as the area beneath a force-position graph).
In my description of how we do the energy “cheat sheet”, I talk about our crude thinking of energy as pain.
I’m not sure I understand what you’re talking about when you say “impact testing from different heights”.
Sounds like we do about the same thing! I do pur charts right after defining energy and caregorizing flavors. ( storage forms). I do the usual modeling worksheets afterwards.
I have seen impact testing labs with sand pits and objects dropped onto them . . . kinda visual energy is pain / change.
I’ll put my energy diagramming reading pages on the interwebs sometime.
Are you still doing energy first? If so, do you still do the “area beneath the force-position graph” so early in the year? I’m trying to think of a simple experiment to do with energy before we get to to quantitative expressions for various flavors of energy. Then I’ll use interactions (systems thinking) and energy as themes throughout the year. Brunschwig’s two operational definitions of energy ( http://fernwig.org/start.php?case=display_chapter&chapter=chapter009&chapter_no=9 ) as (1) 1 Joule = lifting 0.1kg vertically by 1m and (2) 1 Calorie = melting 0.0125 kg of ice look promising and would probably help students with proportional reasoning.
I suppose I could still do force-position graph as I have in the past if many students come in with some understanding of force. However, last year I had trouble finding light-enough and weak-enough springs to launch my carts. Also, my springs were non-Hookian. Instead, we developed a spreadsheet simulation of two carts launched by two different springs (which relied on the Unbalanced Forces Model so I can’t do it this time around). Once the students adjusted the simulated spring displacement to match the final velocities of the carts and plotted their results on the force-position graph, they figured it out in about 10 minutes. I’ve seen your pictures of carts pulled by springs, but my I definitely haven’t been able to make it work quite as well. Any tips?
I am doing a new sequence in my regular physics class. It will not have the experiment you’re talking about in the first semester. It will not use those definitions. But I’m also not yet ready to share what I’m doing with that class. Sorry.
Great textbook source! I think Brunschwig would want you to know, though, that he has simply edited this text which was written by his mentor, Robert Karplus. The amount of work that Fernand has done in publicizing and making the text and its key ideas accessible has been pretty monumental though, so I think they both deserve credit 🙂
Thanks, Lucas. My attribution was lazy there. Yes, Robert Karplus wrote an amazing text, and we can all thank Ferdinand Brunschwig for keeping it alive.
[…] in mind. So where should we start then? As always, the blogosphere has the answer. I found this post by Kelly O’Shea. Starting with pie charts? Sounds good to me. Maybe that will help us gain a better […]
Thanks for the rundown on pie chart introduction. It is a huge help. This is my second year starting with energy in my accelerated physical science class (9th grade). We basically do physics first and a little chem. I’ve seen other just use E diss for thermal energy? Do you distinguish between E therm, E diss, and E int before this? I’m a new physics teacher, so please excuse if there is something basic I am missing.
Just found this, helped a ton with my homework over this. Oddly enough, it looks like my teacher uses your blog to teach all the time. 😂 Thanks for explaining this.
That’s awesome! Say “hi” to your teacher for me!